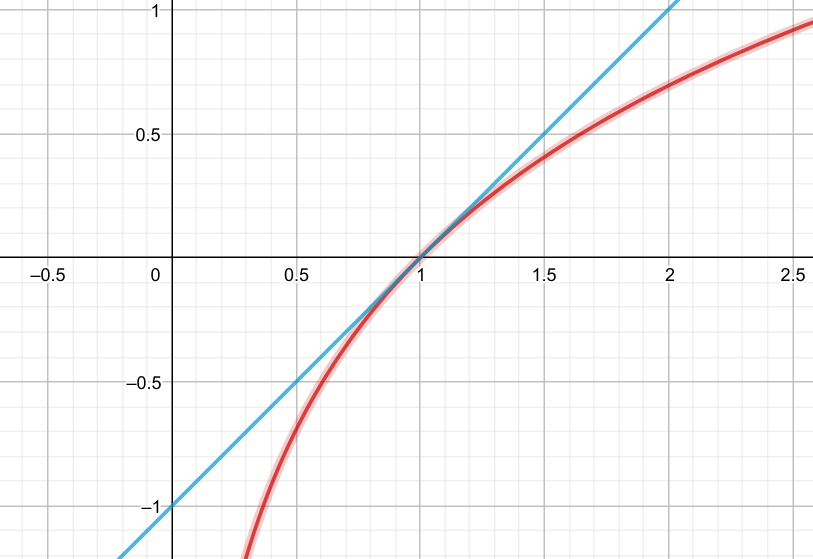
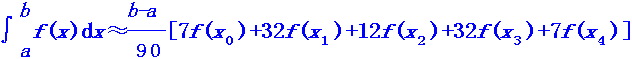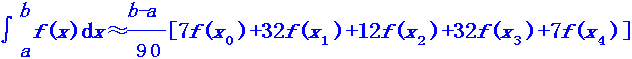前言
最近做数学卷,有一道题我最后化简出来的结果是 $\frac 9 {lg4}$,于是我脑子一热,$lg4$绝壁小于0.5!然后就炸了……
于是我就在考虑估算如何对数的问题
初步
先拿$ln2$举例
最简单的方法就是利用常见不等式: $$ lnx \le x-1 $$ 于是: $$ ln2 \le 2-1=1 $$ 不过这也太不精确了吧!有没有什么方法可以让它精确一点呢?
注意到上述不等式取等条件为 $x=1$ ,那就是说x越接近1,用它算出来的结果越精确
那怎么样才能让x接近1呢?
利用对数的性质
$$
ln(ab)=lna+lnb
$$
可得
$$
ln(x)= ln(\frac {bx} a ·\frac a b)=ln \frac {bx} a + ln \frac a b
$$
只要选取合适的a,b,就可以让 $\frac {bx} a$ 和 $\frac a b$ 都接近1,这不就能更精确了吗?
尝试一下: $$ ln2=ln\frac 4 3 ·\frac 3 2=ln\frac 4 3+ln\frac 3 2\le \frac 4 3-1+\frac 3 2 -1=\frac 5 6 $$ 这不就精确多了吗?
但这个误差还是有点大,如何再精确点呢?
聪明的你肯定想到了,只要拆成更多项,不就能更精确了嘛~
说干就干
$$
ln2=ln({8\over7}·{7\over6}·{6\over5}·{5\over 4})\le {1\over7}+{1\over6}+{1\over5}+{1\over4}=0.7595
$$
聪明的你肯定已经发现了规律
$$
lnx\le {1\over ax-1}+{1\over ax-2}+…+{1\over a}=\sum_{i=1}^{ax-1}{1\over i}
$$
x=2时,取a=200,得
$$
ln2\le 0.6943987
$$
已经离真实值ln2=0.69314718很接近了!
进阶
但是这计算量也太大了!谁会闲着没事算几百个分式的和?还能不能改进一下呢?
想想看这种方法还能优化啥?是不是只剩优化不等式了?
对嘛,换个准一点不等式的不就好了?
比如
$$
lnx\ge {2(x-1)\over x+1},(x\ge 1)
$$
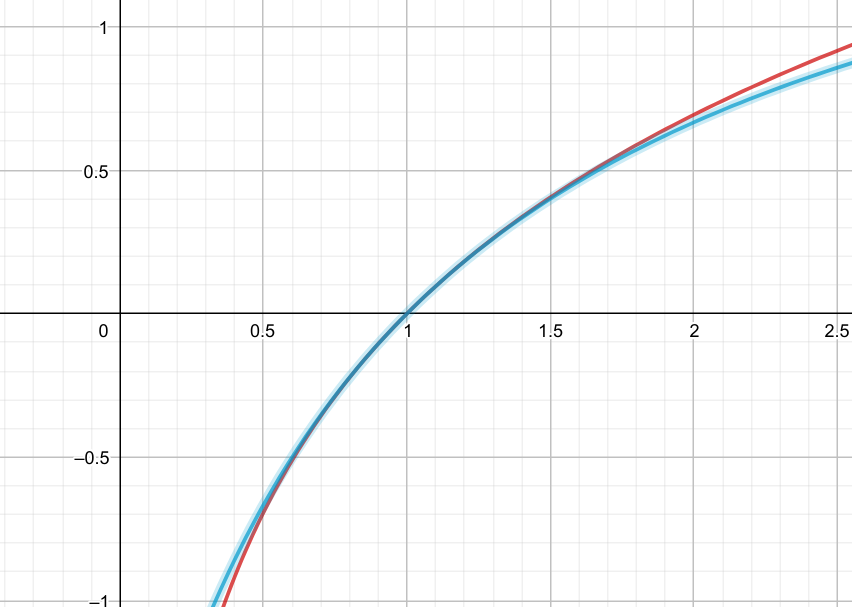
仍然在x=1取等,还是熟悉的配方!
于是同理可以得出
$$
lnx\ge \sum_{i=a}^{ax-1}{2\over 2i+1}
$$
令x=2,a=10,得
$$
ln2 \ge 0.69283536
$$
这10项算起来已经比原来200项的效果都要好了!
如果你比较擅长徒手开平方,甚至还可以试试更准的
$$
lnx\le \sqrt {x}-\sqrt{1\over x},x\ge1
$$
依然是x=1时取等
也就是说
$$
lnx\le \sum_{i=a}^{ax-1}\big (\sqrt{i+1\over i}-\sqrt{i\over i+1}\big )
$$
令x=2,a=6,得
$$
ln2 \le 0.69357944
$$
用6项取得了同样的效果!
dalao们的方法
作者:王希
链接:https://www.zhihu.com/question/25485897/answer/46701302
来源:知乎
高中生除了 @王筝 提到的转化成黎曼和的方式之外没有别的办法了。但是在大学,转化成定积分之后有更好的方法。
1.辛普森公式:
也就是说
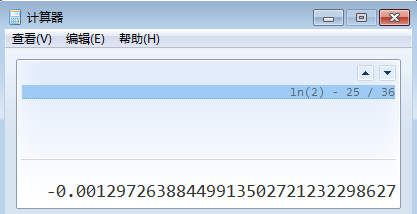
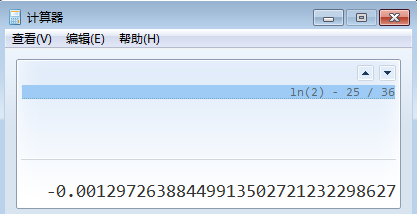
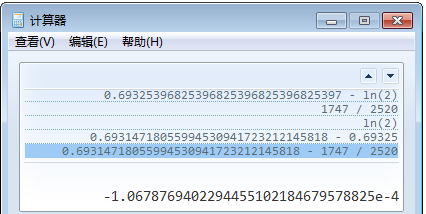
用计算机检验误差:
只有3位,怎么办呢?没关系,我们可以等分区间,然后对两侧的区间分别应用辛普森公式,再加起来。
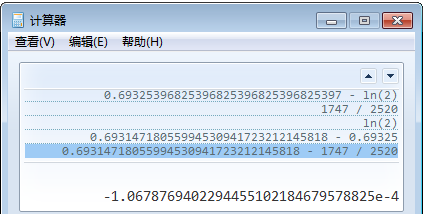
这次的误差就足够小了
2.另外,还可以直接用科特斯公式
计算,结果应该更准确。
作者:王筝
链接:https://www.zhihu.com/question/25485897/answer/30862922
来源:知乎
楼上两位说的当然是对的,但是收敛太慢了,算到精确到4,5位要算很多项才行。
给一个收敛稍微快一点的。